[Introduction]
Data Entanglement란?
Data Entanglement란 데이터 얽힘이라는 의미로 본 논문에서는 두 개 이상의 모달리티에 대한 데이터가 서로 섞여있는 상태를 말한다. 시계열을 처리하는 방법들 중에 LLM을 활용하는 방법들이 제안되고 있는데 최근 제안된 연구들에서는 모두 데이터 얽힘 문제가 발생한다고 지적하고 있으며 본 논문의 방법론인 TimeCMA를 통해 이러한 데이터 얽힘 문제를 해소하였다라고 주장하고 있다.
[Method]
Model Structure

제안하는 TimeCMA 모델은 크게 네 가지 부분인 입력, 인코딩, Cross Modality Alignment, Time Series Forecasting으로 나눌 수 있다.
Input
입력 부분에서는 다변량 시계열에 대해서 시퀀스 길이 만큼 각각의 단변량 시계열에 대한 프롬프트를 생성한다. 프롬프트 형식은 위 Structure에 나와있는 형태로 구성한다.
Dual-Modality Encoding
각 시계열에 대한 프롬프트를 생성하고 나면 각 모달리티에 대한 인코딩을 수행한다. 시계열 데이터는 Inverted Embedding이라는 걸 수행하게 되는데 이는 L 길이의 시퀀스 길이에 대한 시계열을 압축한 C 길이의 임베딩 벡터로 변환하는 작업이다. 이를 통해 임베딩을 수행하고 Time Series Encoder를 통해 각 변수 간 관계를 고려하여 임베딩 벡터를 생성한다.
각 프롬프트에 대해서는 디코더 기반의 LLM을 통해 임베딩을 1차적으로 수행하게 되는데 이때, 본 논문의 논리는 LLM2vec이라는 논문에서 제안한 것처럼 디코더 기반 LLM도 인코딩으로써의 능력을 입증(?)했다고 주장하며 이러한 인코딩을 수행한다.(LLM2vec이라는 논문을 읽어보면 알겠지만 디코더 기반 LLM이 이러한 능력이 있다는 걸 말하고 싶은게 아니라 디코더 기반 LLM에 어떠한 처리를 통해 인코딩을 수행하도록 할 수 있다고 주장한다. 이 부분이 조금 어색하긴 했다.) 그래서 변환된 토큰들 중에 LLM이 출력한 마지막 토큰은 입력에 사용된 모든 정보를 보고 그 정보가 압축된 토큰이므로 본 논문에서는 이 마지막 토큰만을 활용한다. 이후 Prompt Encoder를 통해 각 변수 관계를 고려하여 임베딩 벡터를 생성한다.
두 인코딩에 사용된 Encoder는 모두 PreLN의 트랜스포머 구조를 사용하였다.
Cross-Modality Alignment
본 논문에서 주장하는 이 Data Entanglement 문제를 해결한 주요 모듈인 Cross-Modality Alignment(CMA) 모듈이다. 현재까지는 시계열에 대한 두 표현 (시계열, 프롬프트)에 대해 임베딩을 수행하였고 각각 변수별 임베딩 벡터로 표현된 상황이다. 본 논문에서 제안한 이 모듈은 해당 다변량 시계열을 표현하는 두 표현의 임베딩 벡터 간의 유사도를 비교한다. 예를 들어, A라는 변수의 패턴을 표현한다고 해보자. 그러면 A 변수를 표현하는 임베딩 벡터와 다른 방식으로 표현된 A 변수에 대한 유사도를 비교하지만 본 논문에서는 각 임베딩 벡터들이 각 변수를 표현하는 표현에 대해서 비교하고 다변량 시계열을 표현하는 임베딩 벡터 간의 유사도를 비교한다. (이해가 잘 될 지 모르겠다..)
수식적으로 설명하자면 보통은 N x d, N x d로 각 변수를 표현하는 임베딩 벡터인 d 표현에 대한 유사도를 비교하게 되는데 본 논문에서는 이를 뒤집어서 d x N, d x N으로 각 변수들을 표현하는 임베딩 벡터 간의 유사도를 비교하게 된다. 여기서는 설명을 쉽게 하기 위해서 두 표현에 대한 임베딩 벡터의 차원을 d로 동일하게 표현하였지만, 실제 모델에서 사용된 유사도 비교는 C x N, E x N으로 각 변수를 표현하는 임베딩 차원의 수가 다르다.
이런 식으로 임베딩 벡터의 표현 유사도를 비교하여 시계열 표현에 대한 Residual을 추가하게 된다. 저자들은 이러한 과정을 통해 시계열 표현에서 프롬프트 표현에 대해 필요한 정보만을 찾아서 반영하게 되어 Data Entangle 문제를 해결한다고 주장한다.
Time Series Forecasting
CMA로 출력된 값을 Multivariate Transformer Decoder를 통해 변환을 수행한다. 이후 Projection을 통해 시계열 예측을 수행하게 된다.
[Experiment]

실험 결과를 보면 대부분의 데이터셋에 대해서 SOTA의 성능을 보임을 입증하였다.

FRED와 ILI 데이터셋에 대해서 Ablation Study를 진행하였다. 결과로는 Alignment를 제거하였을 때 가장 성능적인 저하가 많이 발생한 것을 볼 수 있다.
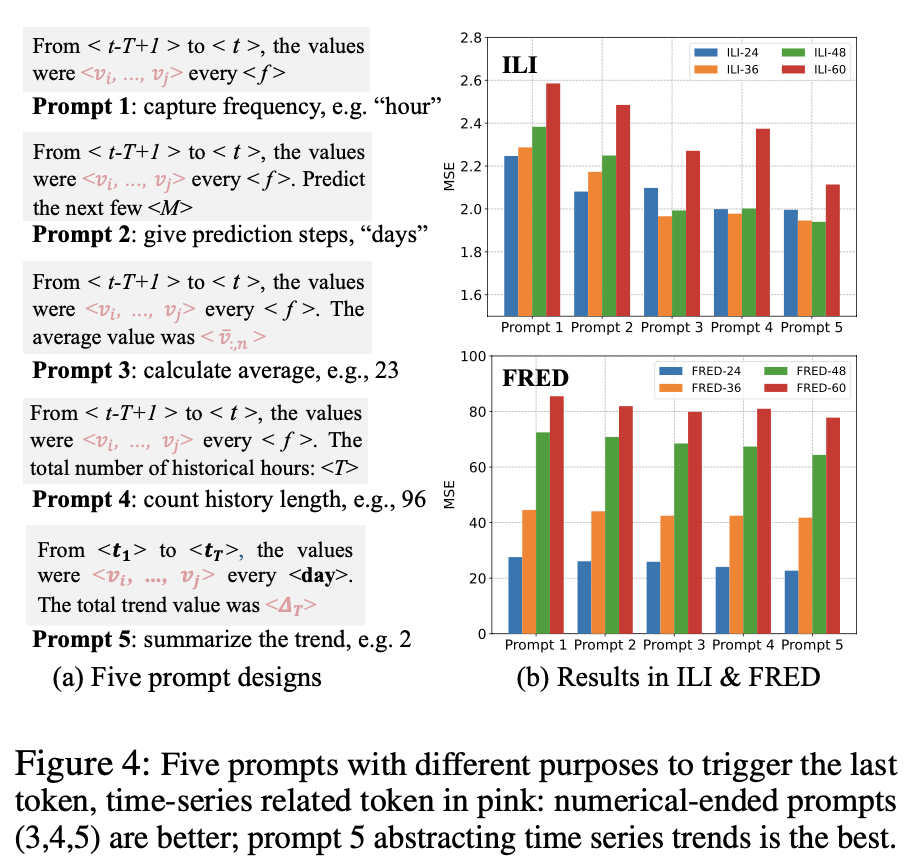
또 다양한 프롬프트를 구성하여 프롬프트에 따른 성능을 평가하였는데, 마지막 값에 숫자를 넣는 프롬프트가 우수한 성능을 보인다고 주장한다.
[Conclusion]
본 논문은 시계열과 LLM에 대한 두 가지 모달리티의 표현에 대해서 Cross Modality Alignment를 통해 기존 연구들의 한계점인 데이터 얽힘 문제를 해결하고 성능적으로 우수한 결과를 보여주었다. 다만 연구에 대해서 깊이 있게 고민하면서 이런 식의 Alignment가 정말 합당한 건가 싶었다. 보통 우리가 생각하는 Alignment는 동일한 패턴에 대한 두 가지 표현에 대해서 한 표현을 다른 표현에 맞게 정렬하는 형태인데 여기서는 아예 모든 변수를 표현하는 공간에 대한 유사도를 비교한다. 이는 어떠한 패턴의 입력이 들어와도 이를 강제로 맞추게 할 수 있기 때문에 우연한 일치로 그 표현 공간이 일치하게 되면 오히려 불필요한 정보임에도 필요한 정보로 인식할 수 있는 위험성이 존재한다고 생각한다. 또한 본 논문에서 제안한 CMA가 실제 다른 연구들에서 나타난 데이터 얽힘 문제를 해결한다는 것을 입증하지 않았다. SOTA의 성능을 달성했다고 Data Entanglement 문제를 해결했다고 볼 수 없기 때문에 이에 대한 자료가 좀더 자세히 있지 않은 것이 아쉬웠다. 뿐만 아니라 현재 많은 연구들이 LLM은 시계열을 처리하는 능력이 없다고 보고되고 있다. 그럼에도 불구하고 해당 논문에서는 시계열에 대한 raw한 표현을 어떠한 처리 없이 LLM을 통해 인코딩하고 있다. 여기서 임베딩 벡터로 변환된 표현은 정말 시계열에 대한 정보가 충분한 것인가? 라는 사실에 대해서 본 논문에서는 증명하고 있지 않다. 실제 본 논문에서 주장하는 LLM의 출력 토큰 중 마지막 토큰 만을 사용해도 충분히 시계열에 대한 Attention이 잘 이루어 지고 있음을 시각화하여 보여주지만 이에 대한 자료의 신뢰도가 적다고 생각한다. 왜냐하면 실제로 마지막 토큰에 대한 어텐션에 대해서 시계열 데이터에 어텐션이 강하게 이루어진다고 한다면 모든 시계열 표현에 어텐션이 강하게 이루어진다는 것이 말이 안되기 때문이다. 어떠한 표현의 편리함 때문에 기존 프롬프트 형태로 표현한 것이겠지만 이에 대한 좀더 명확한 설명이 필요하다고 생각하였다. 추가적으로 본 논문에서는 시계열 인코더는 locality한 특징, 프롬프트 인코더는 global한 특징과 전반적인 관계를 나타낸다고 주장한다. 시계열 인코더가 각 변수간 관계를 나타낸다는건 자명하다. 다만 프롬프트 인코더에 대해 시각화한 부분을 보게 되면 이 특징이 이해가 되지 않는다. 물론 내가 이해력이 부족해서 그런 것일 텐데.. 아무리 생각해도 시계열의 전체적인, global한 특징이라는 것이 뭘 의미하는 것이며 이러한 부분이 왜 나타났는지에 대한 해석이 부족하다고 생각하였다. 분명 이 인코더는 변수 관계를 나타내는 인코더일 텐데 모든 변수들이 모두 동일한 관계를 가지는 시각화 결과인게 오히려 나는 학습이 원하는 방향으로 이루어지지 않은 것이 아닐까 싶다. 그래서 Cross Modality Alignment를 통한 성능 향상이 아닌 결과값이 CMA 이후 추가적으로 더해주는 Residual에 의존한 성능으로 해석하였다.
논문을 읽으면서 자료가 부족하다는 생각이 많이 들었는데 그럼에도 해당 논문이 우수한 학회인 AAAI에 통과된 논문이라면 내가 고려했던 부분에 대해서 다른 리뷰어들은 고민하지 않았는지 궁금했고 내가 틀렸을 확률이 높기 때문에 아직 공부가 많이 필요하다고 생각이 들었다..
혹시 해당 논문을 읽으신 분들이 있으시다면 위 부분에 대해서 어떻게 생각하는지 댓글로 남겨주시면 감사하겠습니다..!