[Background]
푸리에 변환
● 고속 푸리에 변환 (Fast Fourier Transform)
푸리에 변환은 이산 푸리에 변환(DFT)와 고속 푸리에 변환(FFT)가 있지만 현재는 FFT가 일반적으로 사용된다. 그 이유는 고속 푸리에 변환은 이산 푸리에 변환의 시간 복잡도를 줄인 알고리즘이기 때문이다. 이산 푸리에 변환은 의 시간복잡도를 가지는 반면, 고속 푸리에 변환은 의 시간복잡도를 가진다.
계산 효율을 비교한 그래프는 다음과 같다.

푸리에 변환에 대해 간단하게 설명하자면 시간에 따라 측정된 신호를 주파수 영역으로 변환하는 방법이다. 즉, 모든 신호는 여러 개의 사인파와 코사인파의 합으로 표현 가능하다는 것이다. 이는 신호 처리, 이미지 처리, 시계열 데이터 분석 등 다양한 분야에서 활용될 수 있다.
Post-LN vs Pre-LN
● Post-LN - (a)
Post-LN은 Attention is all you need로 세상에 트랜스포머를 알린 논문에서 제안된 방법으로 입력 데이터에 정규화를 거치지 않고 Attention을 수행하고 이후에 Skip connection인 addition과 LayerNorm으로 입력 정규화를 수행하는 방법이다. 해당 방법은 현재 성능이 우수하다고 평가되지만 학습 과정에서 Warm-up 과정이 필수로 요구되고, 깊이 있는 네트워크의 경우에는 학습에 어려움이 존재한다는 한계점이 존재한다. 이러한 한계점을 해결하고자 제안된 방법이 Pre-LN이다.
● Pre-LN - (b)
Pre-LN은 입력 데이터에 대해 먼저 정규화를 수행하고 Attention을 수행하는 과정으로 아래 그림의 (b)에 해당한다. 해당 방법은 간단한 구조 변경만으로도 학습을 기존 Post-LN보다 안정적으로 수행하며 Post-LN과 달리 Warm-up 과정이 필요하지 않다는 장점을 가지고 있다.

[Summary]
최근 시계열 이상탐지 연구에서는 재구성 기반 이상탐지와 예측 기반 이상탐지 연구가 중점적으로 수행되고 있다. 재구성 기반 이상탐지 방법에서는 주파수 변환을 이용하여 시계열의 이상을 탐지하고자 하는데 제안된 방법들은 Coarse-grained 관점에서 주파수 데이터를 이용하여 이상탐지를 수행한다. 하지만 그렇게 되면 저주파수 영역에 속한 이상탐지는 잘 수행하지만 고주파수 영역에 속한 이상에 대한 탐지 성능을 떨어지게 된다.
또한 최근 다변량 시계열 이상탐지에서는 채널간의 관계를 고려하지 않는 방법인 CI(Channel-Independent)와 CD(Channel-Dependent)를 선택하여 사용하고 있는데, CI의 경우, 각 변수에 대해서 모델이 강건하게 이상탐지를 수행하지만 다른 변수가 미치는 영향에 대해서는 고려하지 않는다. CD의 경우, 각 변수들 간의 관계를 고려하고 있지만 관계성이 약한 변수들도 고려한다는 점에서 오히려 노이즈가 발생할 수 있다.
따라서 본 논문에서는 Coarse-grained관점이 아닌 Fine-grained 관점에서 주파수 영역을 다루며 CI와 CD의 밸런싱을 적용한 모델인 CATCH를 제안한다.
Structure
전체 모델 구조는 크게 세 부분으로 나눌 수 있다.
Forward Module
- Instance Norm : 변수간의 데이터 분포를 보장하고 학습과 평가의 분포가 다른점을 고려하여 정규화 수행하는 RevIN 적용.
- FFT & Patching, Projection : 정규화된 데이터에 대해 푸리에 변환을 적용하고 실수부와 허수부를 각각 패칭을 적용한다. 패칭을 적용한 후 각 영역별로 Concatenate하고 d차원으로 Projection한다.
Channel Fusion Module
논문에서 주장하는 핵심 부분으로 Mask Generator, Channel-Masked Transformer, Channel Correlation Discovering 으로 구성된다.
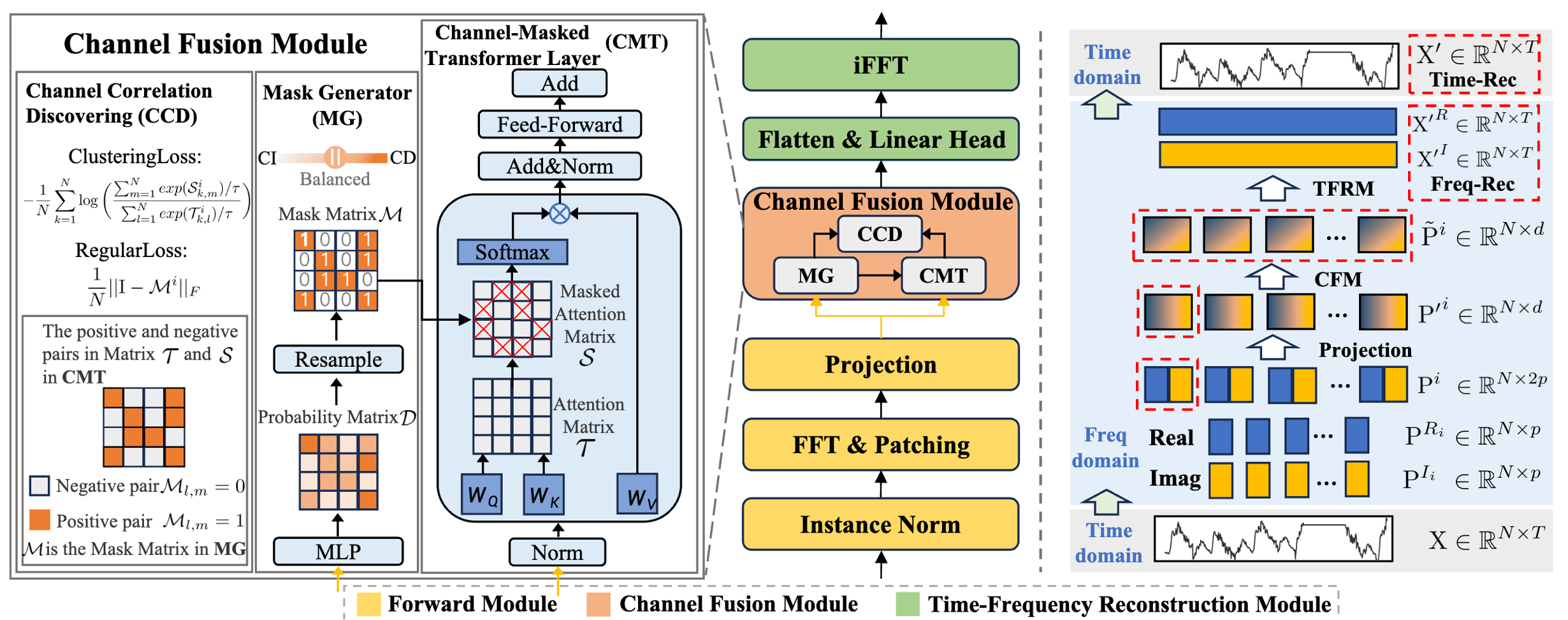
- Mask Generator : Forward Module로 얻은 N x d차원의 표현들을 N x N 차원으로 변환한다. 이를 통해 각 변수가 미치는 영향을 확률 Matrix 로 표현한다. 확률 Matrix를 그대로 적용하지 않고 Gumbel-Softmax를 통해 이진화를 수행한다. 이때, 기본적인 Threshold로도 이진화를 할 수 있는데 Gumbel-Softmax를 사용한 이유는 일반적인 Threshold로 구분하면 이는 미분이 불가능하기 때문에 역전파가 불가능하다. 따라서 역전파가 가능하도록 이를 확률적인 관점으로 풀어 Softmax trick을 사용하여 학습이 가능하도록 설계한다. 원래 Gumbel-Softmax는 다분류에서 적용될 수 있지만 본 논문에서는 이진 분류만을 수행하기 때문에 기본적인 Gumbel-Softmax의 확률 부분을 odds로 구성하여 로짓으로 구성하여 더욱 효과적으로 학습하도록 한다. 추론 시 Gumbel Softmax가 아닌 일반적인 threshold를 사용하여 구성한다.

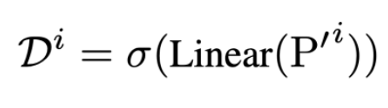


- Channel-Masked Transformer : Pre-LN의 구조를 차용하여 입력 시계열 표현을 학습을 수행한다. 이때, 이후에 사용되는 CCD에서 Masked Attention 결과와 Attention 결과 비교가 필요하므로 Attention을 여러 번 수행하는 것이 아닌 Full Attention 후에 Masking을 적용하는 방법을 채택한다. Masking을 적용할 때 Softmax 연산에서 0은 의미를 가지기 때문에 이를 -무한대를 곱해 영향을 없앤다.
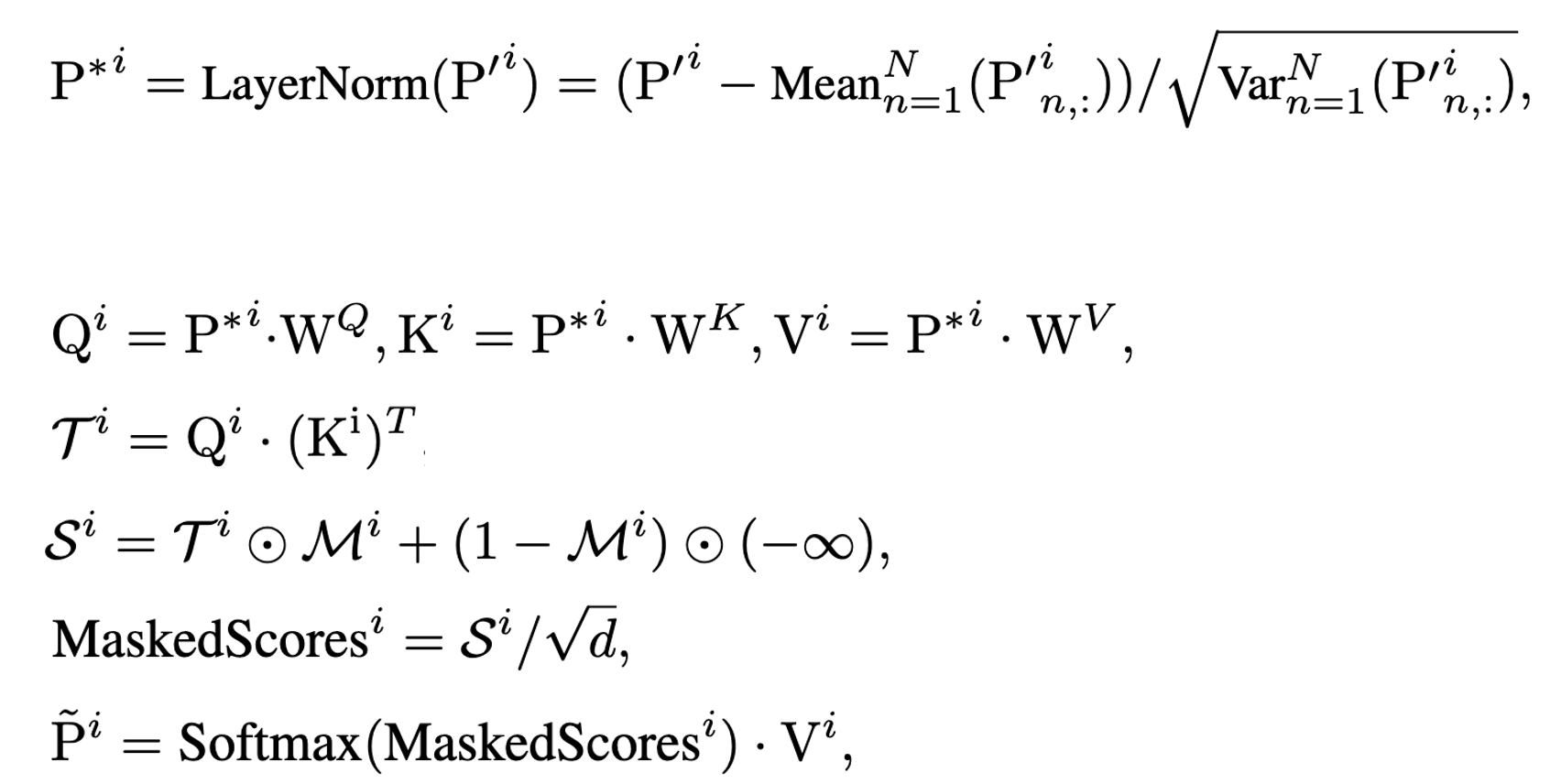
- Channel Correlation Discovering : 이제 마스킹이 잘 적용될 수 있도록 두 가지 Loss Function을 구성한다.
- Clustering Loss : Masking 어텐션 결과와 어텐션 결과의 표현을 분석하여 실제 해당 변수의 영향이 큰지에 대한 Loss Function으로 변수 간의 관계를 잘 반영할 수록 Loss 값이 낮아진다. 하지만 Cluster Loss만 적용하게 되면 모든 변수에 대해서 관계가 있다고 단정짓게 되면 Loss가 매우 낮게 나오는 경향이 존재한다. 따라서 다음 Loss를 추가하여 사용한다.
- Regular Loss : Clustering Loss만 사용하면 나오는 문제점을 보완하고자 사용하며 변수 관계를 무분별하게 적용하지 않도록 한다.

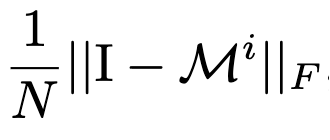
Time-Frequency Reconstruction Module
CMT가 출력한 결과를 다시 시계열로 재구성하는 과정으로 출력 결과를 실수부와 허수부로 분리하고 분리한 결과를 복소 평면에 나타낸 후 나타낸 결과에 대해 Inverse FFT를 수행한다. 수행한 결과에 대해 실수부와 허수부를 추출하는데 그 이유는 모델이 출력한 결과가 이상적인 주기를 가진 사인파와 코사인파의 합으로 나타나지 않을 수 있기 때문에 수행한 결과를 실수부와 허수부로 추출하고 이를 선형변환함을 통해 재구성한다.
Joint Bi-level Optimization
모델이 재구성 학습에서 사용하는 손실은 크게 네 가지 이다. 이전 CMT에서 제안한 CCD 과정에 사용된 Clustering loss와 Regular Loss와 시간 도메인의 재구성 손실과 Frequency 도메인의 재구성 손실, 네 가지를 사용한다. 역전파 학습시, 전체 Loss를 네 손실의 가중합으로 구성하여 전달하며, 이때, 학습의 안정성을 위해 Joint bi-level optimization을 사용한다.



학습시에 마스크에 대한 손실을 먼저 업데이트하고, 업데이트된 마스크를 기준으로 모델을 업데이트하는 과정을 통해 동일 마스크 내 모델의 학습으로 두 단계로 분리하여 학습 안정성을 높이고자 하였다.

Anomaly Scoring

학습된 모델을 사용하여 이상탐지를 수행할 때, 시간 도메인에서의 재구성 오차와 주파수 도메인에서의 재구성 오차를 가중합하여 사용한다. 이를 통해 국소 이상에 대한 결과는 Time-Score를 통해, 넓은 범위에 대한 구간 이상은 Frequency-Score를 통해 보완하고자 하였다. 이때, Frequency score는 high frequecy 부분을 고려하기 위해 각 윈도우 구간을 다시 패치 단위로 나누어 세밀하게 조정하고자 하였다.
[Experiments]
Main Experiment
실험은 총 12개의 실제 데이터셋과 6개의 합성 데이터셋을 사용하였다. 비교 모델로는 최근 SOTA를 달성한 모델부터 전통적인 통계기반의 방법을 사용하였다. 평가 지표는 Affiliated-F1 score와 ROC-AUC를 사용하였다. 아래는 실험 결과표이다.

대부분의 데이터셋에서 SOTA의 성능을 달성함을 알 수 있다. 다만, SWAT 데이터셋 결과에 대해서 저자들은 SWAT 데이터가 해당 모델이 커버하는 이상탐지 범위보다 긴 이상 길이를 가지고 있으므로 성능이 좋지 않다고 주장하였다. (SMAP 데이터셋에 대한 언급은 없음) 이외에 다른 평가 지표에 대한 결과는 Appendix에 추가되어 있으니 관심 있다면 찾아보면 좋을 것 같다.
Ablation Study

본 논문은 제안한 방법에 대해 Ablation study를 진행하였다. Frequency 재구성 오차를 제거했을 때 성능 저하가 가장 많이 일어났다.
[Results]
본 논문은 시계열 도메인에서 주파수 도메인으로 변환하여 시계열 이상탐지를 수행하고자 하였다. 이 과정에서 변수 관계 고려를 위해 Mask-Matrix를 제안하였으며, 해당 Mask Matrix가 변수 관계를 잘 나타낼 수 있도록 다양한 학습 장치를 사용하였다. 또한 기존 주파수 도메인 접근 방법과 다르게 높은 주파수 영역에 대해 다루기 위해 더 세밀하게 평가하고자 하였다.
변수 관계를 고려하기 위해 다양한 방법들이 제안된다. 그래프 기반, 인접 행렬 기반, 어텐션 기반 등 다양한 방법들이 제안되었는데 해당 논문에서 제안한 Mask Matrix는 간단하면서도 효과적으로 변수 관계를 고려한 방법이라고 생각된다. 또한 최근에 시계열 데이터를 주파수 도메인에서 분석하고자 하는 경향이 있고 성능도 우수한 결과가 상당수 존재하기에 다음 논문도 주파수 도메인에서 다뤄본 논문에 대해 읽어볼 예정이다.

