※ 논문을 읽고 개인적으로 정리한 것으로 틀린 해석이 있을 수 있습니다 ※
[Background]
● 연구 의도
Transformer 모델은 입력 시퀀스의 길이가 길어지면 처리하는 데에 시간이 오래걸린다는 단점이 존재한다. 이러한 단점은 장기 시계열 예측에 가장 많이 드러난다. 따라서 본 논문에서는 기존 Transformer의 장기 시계열 예측에서의 문제점을 해결하고자 하였다.
● 시계열 분해 (Decomposition of Time Series)
시계열 데이터를 trend와 seasonality로 나누는 기법이다. 먼저, 원본 시계열에서 trend를 분리한다. 원래 데이터에서 trend를 제거한 값에서 기간 별 데이터의 평균을 통해 seasonal 값을 구한다. 이후 원래 데이터에서 추세와 계절성을 제거하여 잔차값(residual)을 구한다. 이러한 과정을 통해 trend와 seasonality를 구할 수 있다.
● 고속 푸리에 변환 (Fast Fourier Transform)
푸리에 변환은 이산 푸리에 변환(DFT)와 고속 푸리에 변환(FFT)가 있지만 현재는 FFT가 일반적으로 사용된다. 그 이유는 고속 푸리에 변환은 이산 푸리에 변환의 시간 복잡도를 줄인 알고리즘이기 때문이다. 이산 푸리에 변환은 $O(N^{2})$의 시간복잡도를 가지는 반면, 고속 푸리에 변환은 $O(NlogN)$의 시간복잡도를 가진다.
계산 효율을 비교한 그래프는 다음과 같다.
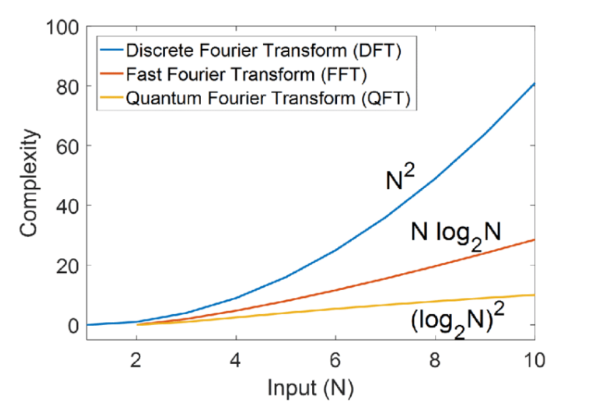
푸리에 변환에 대해 간단하게 설명하자면 시간에 따라 측정된 신호를 주파수 영역으로 변환하는 방법이다. 즉, 모든 신호는 여러 개의 사인파와 코사인파의 합으로 표현 가능하다는 것이다. 이는 신호 처리, 이미지 처리, 시계열 데이터 분석 등 다양한 분야에서 활용될 수 있다.
추세를 구하는 방법에 따라 달라지는데 본 논문에서는 Moving average를 이용하였다.
[Summary]
본 논문에서는 복잡한 패턴 처리, 효율적 계산을 위해 다음과 같은 방법을 제시한다.
복잡한 패턴 처리를 위해서 시계열 데이터를 추세(trend)와 계절성(seasonality)로 분해하여 처리한다.
Auto-Correlation 메커니즘을 사용하여 종속성을 학습하고 계산 효율성을 높인다.
Autoformer의 전체적인 구조는 Transformer 모델의 Encoder-Decoder 구조를 기반으로 설계되었다.

Decomposition Architecture
장기 시계열 예측에서 복잡한 패턴을 학습하기 위해 이전 연구의 시계열 분해 방법을 사용한다. 하지만 미래 시계열 데이터는 우리가 모르기 때문에 모르는 데이터를 분해할 수는 없다. 따라서 Series Decomposition block을 통해 점진적으로 seasonal과 trend를 분리하여 학습하도록 한다. 이를 위해 이동 평균(Moving Average)를 적용하여 주기적인 변동을 안정화하고 long-term trend를 효과적으로 학습하도록 한다. 수식은 아래와 같다.
$$ \chi _{t} = AvgPool(Padding(\chi)) $$
$$\chi_{s} = \chi - \chi_{t} $$
Auto-Correlation Mechanism
Transformer 모델에서 사용하는 Self-Attention을 대체하여 시계열 데이터의 주기적 패턴과 장기 의존성을 효과적으로 학습하는 데 사용된 방법이다.
Why?
Self-Attention 대신에 쓴 이유는 Self-Attention의 계산이 $O(L^{2})$의 시간복잡도를 가지고 있기에 이를 피하면서도 시계열 데이터의 주기적 패턴과 장기 의존성을 효과적으로 학습하기 위해 위 방법을 도입하였다.
Methodology
시계열 데이터의 자기상관 함수를 활용하여, 특정 시간 지연에 따른 데이터 간의 상관 관계를 계산하고 데이터 내 주기적 패턴을 학습한다.
1. Auto-Correlation

Auto-Correlation은 시계열의 Lag들에 따른 자기유사성을 측정하는 함수이다. Autoformer는 이를 통해 중요한 Lag 들을 찾아낸다.
$$R_{XX}(\tau) = \frac{1} {L}\sum_{t=1}^{L}X_{t}\cdot X_{t-\tau}$$
$R_{XX}(\tau)$ : 시간 지연 $\tau$에서의 자기상관 값
$X_{t}$ : 시계열 데이터의 t번째 값
$X_{t-\tau}$ : $\tau$만큼 시간 지연된 데이터 값(Lag)
2. Time Delay Aggregation

자기 상관 값이 높은 Lag들을 선택하여 해당 시간 지점에서의 데이터와 현재 데이터를 결합한다. 선택된 Lag들은 Auto-Correlation의 계산 결과를 기반으로 중요도가 높은 순서대로 결정된다.
-> 어텐션을 통해 관계가 높은 시계열에 높은 중요도를 부여하는 것과 유사

3. Fast Fourier Transform (FFT) 활용
내용은 Background 참고. 이를 통해 자기 상관 계산을 $O(LlogL)$의 시간복잡도로 수행가능하고 기존 Self-Attention보다 효율적으로 계산한다.
Wiener-Khinchin 정리
신호의 자기상관 함수와 주파수 스펙트럼이 푸리에 변환 관계를 가진다는 것을 의미하는 정리. 이는 Autoformer에서 Auto-Correlation을 계산할 때 FFT를 활용하는 이론적인 근거를 제공한다.
Input
모델의 입력은 다음과 같이 주어진다. 본 논문에서는 Encoder의 입력이 과거 I timesteps 만큼을 입력한다고 하였지만 실제로 입력되는 부분은 $ \frac{I} {2}$ 부터 $I$까지이다. 이렇게 한 이유는 최근 정보들을 제공하는 것이 예측을 잘 수행하기 때문이라고 한다. 그렇다면 $\frac{I}{2}$ 이전의 데이터는 필요 없는 건가? 라고 생각이 들었는데 이 부분은 Decoder 부분의 trend를 계산할 때 평균을 통해 계산되어 간접적으로 영향을 준다.

Encoder
Encoder 부분은 위의 그림에 자세히 나와있다. 첫 입력 부분은 위에서 설명한 것처럼 입력 시계열 데이터가 그대로 입력되는 것이 아니라 $ \frac{I} {2}$부터 $I$까지의 데이터를 시계열 분해한 후 Seasonal 부분만 Encoder의 입력으로 사용된다. 이후에는 이전 Encoder의 결과가 다음 Encoder의 입력으로 사용된다. 구체적인 수식은 아래와 같다.
$ S^{l,1}_{en}, $ _ $ = SeriesDecomp(AutoCorrelation(\chi^{l-1}_{en}) + \chi^{l-1}_{en}) $
$ S^{l,2}_{en}, $ _ $ = SeriesDecomp(FeedForward(S^{l,1}_{en}) + S^{l,1}_{en}) $
여기서 $l$은 Encoder의 레이어를 의미하고 $l$ 옆의 숫자는 해당 레이어의 몇 번째 Series Decomposition block인지 나타낸다. 이러한 과정을 N번 반복한다.
Decoder
Decoder 부분도 위의 그림에 자세히 나와있다. 첫 입력은 아까 설명한 것처럼 trend와 Seasonal, 두 가지로 나뉘어서 입력된다. trend 부분은 입력 시계열 데이터의 trend와 입력 시계열 데이터의 평균을 Concat하여 입력하고 Seasonal 부분은 입력 시계열 데이터의 Seasonal과 0을 Concat하여 입력한다. 이후에는 이전 Decoder의 결과가 다음 Decoder의 입력으로 사용된다. 구체적인 수식은 아래와 같다.

여기서 $l$은 Decoder의 레이어를 의미하고 그 뒤의 숫자는 해당 레이어의 몇 번째 Series Decomposition block인지 나타낸다. 하나의 Decoder 레이어를 통과하고 나면 각 Series Decomposition block을 거친 결과의 trend를 합쳐서 해당 레이어의 trend로 concat해야 한다. 이때 $W_{l,i}, i \in {1, 2, 3}$은 i번째 trend의 가중치 행렬이다. 이러한 과정을 M번 반복한다.
마지막 예측은 분리된 trend와 seasonal 결과값을 $W_{S} * \chi^{M}_{de} + T^{M}_{de}$로 합하여 최종 예측한다.
[Results]
● 데이터셋
ETT, Electricity, Exchange, Traffic, Weather, ILI 데이터셋으로 실험을 진행하였다.
● 예측 길이
{96, 192, 336, 720} ( ILI의 입력 길이는 36, 나머지는 96으로 설정)
● 설정
optimizer : ADAM
Batch size : 32
early stop : 10 epochs
train valid test rate : 6:2:2 for ETT and 7:1:2 for the other datasets
Auto-correlation hyper parameter c : 1 to 3
● 비교 모델
multivariate forecasting :
transformer based models : Informer, Reformer, LogTrans
RNN based models : LSTNet, LSTM
CNN based models : TCN
univariate forecasting :
N-BEATS, DeepAR, Prophet, ARIMA
Multivariate results

다변량 시계열 예측에 있어서 Baseline 모델들에 비해 좋은 성능을 보인다.
Univariate results

단변량 시계열 예측에서도 좋은 성능을 보인다.
또한 점진적으로 시계열 분해하는 과정을 적용함으로써 trend를 더 잘 분리해낼 수 있다고 하였다.

[Conclusions]
본 논문은 시계열 예측에 있어서 트랜스포머 모델의 구조를 변형하여 시계열 예측 과업에 맞는 구조로 변환하여 예측하는 방법을 제시한다. 시계열 데이터의 특성인 추세와 계절성을 이용하여 푸리에 변환으로 얻은 주기적 공통성으로 예측한다는 것이 흥미로웠다. 이번 논문을 읽으면서 푸리에 변환에 대해 다시 한번 공부할 수 있는 기회가 되었다. 또한 기존 어텐션 연산 대신에 Auto-correlation을 통해 시간 복잡도를 줄이면서 더 좋은 성능을 보여주었다. 물론 지금의 시계열 예측 방법들에 비하면 낮은 성능이지만 시계열 예측에 있어서 트랜스포머 구조에 전통적인 방법을 접목시키려는 논문이었다고 생각한다.


