[Background]
● CRPS(Continuous Ranked Probability Score)
주로 확률적 예측 모델의 성능을 평가하는 데 사용된다. 예측된 확률 분포와 실제 값 사이의 거리를 측정하여 값이 낮을 수록 예측이 실제 관측치와 비슷하게 나타난다. CRPS는 CDF(Cumulative Distribution Function)을 기반으로 한다.
$$ CRPS(F,x) = \int_{-\infty }^{\infty }(F(y)-1(y\geq x))^{2}dy$$
위 수식에서 F(y)가 예측된 누적 분포 함수(CDF)이고 $ 1(y\geq x) $는 실제 값 x보다 크거나 같은 y에 대해 1을 갖는 인디케이터 함수이다.
[Summary]
본 논문은 LLM으로 시계열 데이터를 예측하는 방법으로 LLMTIME을 제안한다. LLMTIME의 작동 방식은 다음과 같다.
1. Tokenizing
LLMTIME은 시계열 데이터를 LLM이 잘 이해할 수 있도록 해당 데이터를 텍스트로 변환하는 기법을 사용한다. 이때 토크나이즈 방법으로 각 시계열 데이터에 대해 소수점 둘째 자리까지의 수를 문자로 변환하여 나타낸다. 만약 소수점 셋째 자리에도 숫자가 있다면 이는 버린다. 또한 만약 소수점 둘째 자리에 숫자가 없다면 0으로 넣어주어 채운다. 예를 들어, 만약 [0.123, 1.23, 12.3, 123.0] 시계열 데이터가 있다면 이를 "12, 123, 1230, 12300"으로 변환해준다. 해당 논문에서는 GPT-3과 LLaMA에 대해 두 토크나이징 기법을 적용하였는데, GPT-3의 경우, 중간에 공백을 추가하지 않았더니 해당 시계열 데이터를 예측함에 있어서 성능이 매우 낮아지는 것을 확인하였다. LLaMA의 경우, 오히려 중간에 공백을 추가하여 시계열 데이터를 예측하였더니 성능이 더 낮아지는 것을 확인하였다.
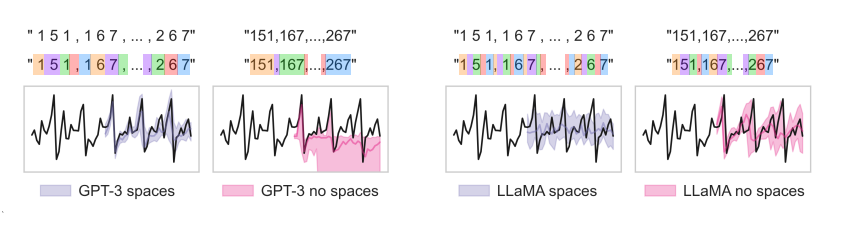
따라서 해당 LLM에 대해 GPT-3의 경우에는 토크나이징 과정에 공백을 추가하도록 하고, LLaMA의 경우에는 공백 없이 토크나이징 하도록 하였다.
2. Rescaling
입력이 매우 클 때, 토큰을 낭비하지 않도록 토크나이징된 시계열 데이터를 리스케일링한다. 이때, $\alpha-percentile$ 방식을 사용한다.
a : $\alpha$ - percentile of the shifted series$(x_{1}-b, x_{2}-b, ..., x_{T}-b)$
$b : min_{t}x_{t} - \beta (max_{t}x_{t} - min_{t}x_{t})$
$min_{t}x_{t} = m, max_{t}x_{t} = M$
$Rescaled\, x_{t} \in \left [ \frac{\beta (M-m)}{a},\frac{(1+\beta)(M-m)}{a} \right ]$
여기서 사용하는 $\alpha$와 $\beta$는 하이퍼파라미터로 $\alpha$는 시계열 데이터의 백분위 값을 기준으로 값을 조정하는 역할을 하며, $\beta$는 데이터의 오프셋을 계산하는 데 사용된다. 이를 통해 시계열 데이터의 특정 값이 지나치게 커지거나 작아지지 않도록 조정한다.
3. Sampling

이 그림은 단순한 자기회귀 모델을 사용하여 복잡한 분포를 학습한 것을 그래프로 나타내고 이의 와서스테인 거리 값을 계산한 결과이다. 그림을 보면 Decimal AR은 단순한 자기 회귀 모델임에도 불구하고 와서스테인 거리를 기준으로 다른 모델들보다 좋은 성능을 보였다. 이를 통해 LLM 또한 복잡한 분포를 학습함에 있어서 좋은 성능을 보여줄 것으로 예상할 수 있다.
LLMTIME 모델은 시계열 데이터를 예측할 때, LLM이 각 입력에 대해 조건부 확률 분포를 계산하고, 계산한 값으로 상위 k개의 값을 추출합니다. 이때 리스케일링한 데이터에서 LLM이 조건부 확률을 계산해서 이산 확률 분포로 나타내고, 이 중 확률이 높은 데이터를 기반으로 선택한다.
샘플링 기법은 이때 사용되어 결과 값의 다양성을 조정하거나 가장 가능성 높은 값들을 선택하는 역할을 한다. 샘플링은 단순히 한 번의 예측을 수행하는 것이 아니라 같은 입력에 대해 여러 번 예측을 반복하는 과정이다. 일반적으로는 20개의 샘플을 생성하는 방식이 사용된다. LLMTIME에서는 세 가지 샘플링 기법을 사용한다.
- 온도 스케일링 : 대부분의 샘플링 과정에서 자주 사용된다. 특히 모델이 더 다양하거나 덜 다양한 예측을 하도록 유도할 때 사용되며, 예측의 탐색-활용 균형을 맞추는 중요한 역할을 한다. 온도 값이 낮으면 모델이 결정론적으로 동작하고, 높으면 더 많은 가능성을 탐색하게 된다. 일반적으로는 0.7로 설정한다. 범위는 0.1~2.0이다.
- 로짓 비편향 : 특정 값이 더 많이 예측되거나 덜 예측되도록 하는 도구로 모든 샘플링에 항상 사용하진 않는다. 예를 들어, 특정 값이 지나치게 자주 등장할 때, 이를 조정하기 위해 사용한다. 이는 특정 패턴이나 편향을 조정하고자 할 때 선택적으로 사용된다.
- 핵심 샘플링 : 상위 확률을 가지는 값들만 선택하도록 하는 기법으로, 불확실성이 큰 시계열 데이터에서 비현실적인 값이 예측되는 것을 방지할 때 유용하다. 데이터가 잡음이 많거나 예측 결과의 품질이 중요할 때 자주 사용되지만, 모든 데이터셋에서 필수적으로 사용되지는 않는다. p값을 설정해서 상위 p%의 값만 선택하게 하며 p는 일반적으로 0.9로 상위 90퍼센트 값만 선택하도록 설정된다.
4. Continuous Likelihood
여기서는 구간(bin) 개념을 도입하여 구간 내 균등 분포를 통해 직접적으로 연속 확률 분포를 구성한다. LLM이 예측한 20개의 샘플링 데이터를 기반으로 구간을 나누어 연속 확률 분포를 구성한다. n개의 숫자로 구성되어 있는 실수의 경우, B진법 기준 $B^{n}$개의 선택지를 갖게 된다. 예를 들어, 10진법의 소수점 두 자리수 까지를 토큰화했으면 아래의 그림처럼 이산확률 모델을 연속확률 모델로 근사하도록 한다.

예를 들어, 위의 그림으로 균등분포를 나누었다고 했을 때, 0.534와 0.537은 둘다 $p_{53}$의 확률에 해당되어 $p_{53}의 확률을 높이게 된다. 이를 통해 연속확률 분포로 나타낸다. 이는 샘플링한 데이터들이 LLM의 예측 성능이 높다면 대부분 오차 범위가 작은 값으로 예측할 것이고 예측한 값에 대해 확률적으로 선택을 해야하기에 연속 확률 분포로 나타낸 것으로 생각된다. 물론 먼 시점의 데이터를 예측하고자 할 때는 샘플링 데이터의 분포가 고르게 되어 있어 여러 확률적 선택을 가능하게 한다는 점에서 좋은 방식을 선택한 것이라고 생각한다.
[Results]
본 논문에서는 LLM의 성능을 비교하기 위하여 LLMTIME의 Foundation 모델을 GPT-3와 LLaMA-2 70B를 사용하였고 뿐만 아니라 전통적인 시계열 데이터 예측 방법과도 성능 비교를 하였다. 성능 평가 지표는 MAE와 Scaled MAE를 사용하였고 데이터셋은 Darts, Monash, Informer로 구성하여 실험을 진행하였다.

위 그래프는 각 데이터셋에 대해 시계열 데이터 예측 방법들을 사용한 결과이다. 대부분 LLMTIME이 좋은 결과를 보여주고 있다.
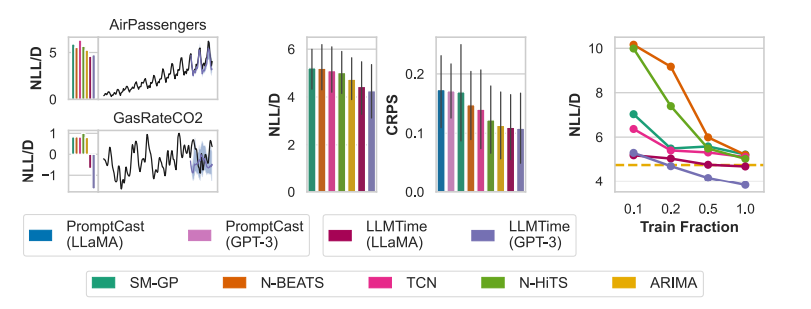
먼저 맨 왼쪽에 있는 그래프는 AirPassengers와 GasRateCO2 데이터셋으로 각 모델의 Negative LogLikelihood/D(차원) 값을 나타낸 것이다. 그래프에서 AirPassengers 데이터셋은 NLL/D값이 잘 계산된 반면, GasRateCO2 데이터셋으로 계산한 NLL/D 값은 음수 값이 나오는 기괴한 결과값을 보여준다.
가운데 있는 그래프는 Darts 데이터셋을 이용하여 각 모델의 NLL/D와 CRPS 값을 계산한 것이다. 두 지표 모두 LLMTIME이 좋은 성능을 보인다고 평가하였다.
마지막 그래프는 제로샷으로 실험을 진행하지 않고 Train 비율을 조절해가며 각 모델의 NLL/D 값을 계산한 결과이다. train 비율이 적을 때는 ARIMA 보다 성능이 낮지만 train 비율을 높일 수록 성능이 향상되는 것을 볼 수 있다.

왼쪽 그래프는 복잡도에 따른 모델 성능을 비교한 그래프이다. 복잡도가 증가함에 따라 훈련 손실, 테스트 손실, LLM NLL 값들이 어떻게 변화하는 지 보여준다. 그래프를 보면 복잡도가 13일 때가 NLL값이 가장 작게 나오면서 가장 잘 맞는다는 것을 보여준다. 또한 LLM NLL 그래프와 Test Loss 그래프가 어느정도 Align되는 것을 보여준다.
오른쪽 그래프는 다양한 함수에 대해 TCN, ARIMA, GPT-3 모델들의 예측 성능을 Log Likelihood로 비교한다. 특히 GPT-3가 복잡한 함수에서도 우수한 성능을 보여준다. 이 그래프들은 LLMTIME의 성능을 측정한 것이라기 보다 LLM이 시계열 데이터를 예측함에 있어서 다른 모델들에 비해 좋은 성능을 보인다는 것을 의미한다.

왼쪽 그래프는 MMLU(한 모델의 종합적인 지능 및 학습 능력을 평가하는 테스트)의 정확도와 NLL/D 및 CRPS 간의 관계를 보여준다. MMLU값이 높아질수록 NLL/D와 CRPS 값이 낮아지는 것을 보여준다. 두 지표 모두 낮을 수록 좋은 지표이다.
가운데 그래프는 GPT-3가 GPT-4보다 시계열 예측 모델에서 더 좋은 성능을 보여준다는 것을 나타낸다. 그 이유로 GPT-4는 언어를 다루는 것에 더 최적화 되어있다고 설명한다.
오른쪽 그래프는 LLaMA Chat 모델이 기본 모델보다 낮은 성능을 보여준다는 것을 나타낸다.
[Conclusions]
본 논문은 시계열 데이터를 예측하기 위해 LLM을 활용한 방법을 제시하고 있다. 이때, 토큰화 과정, 리스케일링 과정을 통해 시계열 데이터를 LLM이 잘 이해할 수 있도록 처리하고, 해당 데이터를 기반으로 LLM은 각 자릿수 별로 조건부확률을 계산하여 얻은 이산확률 분포를 기반으로 확률 높은 데이터를 샘플링한다. 샘플링한 데이터를 기반으로 균등 분포에서 해당 샘플링 데이터를 각 구간에 맞도록 입력하여 연속 확률 분포로 변형하고 그 중에서 가장 확률 높은 데이터를 선택하여 예측을 진행한다. 시계열 데이터를 확률 분포로 나타내어 시계열 데이터를 예측하는 것에 있어서 확률적으로 높은 데이터를 선택한다는 점에서 좋은 방법을 채택한 것 같다고 생각한다. 물론 논문에서 제공한 실험 결과의 그림이 약간의 오류가 존재하였다. 또한 어떤 경우에서는 기본적인 통계 예측 모델인 ARIMA 보다 성능이 낮게 나온 경우도 존재하였다. 좀 더 다양한 데이터셋을 활용하여 예측을 진행했다면 해당 LLMTIME 모델이 좋은 성능을 보여주는 모델이라는 것을 일반화할 수 있을 것 같다.



