[Background]
● Transformer를 이용한 다변량 시계열 예측의 한계
다변량 시계열 데이터를 예측하는 것에 트랜스포머 모델을 사용하는 것이 좋은 성능을 보이면서 트랜스포머 구조를 사용, 활용하여 시계열 예측 과업을 수행하는 연구가 진행중이다. 하지만 여기에는 두 가지 한계점이 존재한다.
첫 번째 문제는 제곱항의 시간 복잡도로 인해 시퀀스 길이가 제한된다는 것이다.
두 번째 문제는 미래 시점의 값을 예측함에 있어서 모든 이전 시점들의 데이터를 활용한다는 것이다. 미래 시점의 값을 예측하는 데에 불필요한 정보들까지 계산함으로써 불필요한 계산과정이 포함된다.
위 두 문제를 해결하고자 해당 논문에서는 Local, Stride, Vary 요소를 이용한 Dozer attention이라는 변형된 어텐션 기법을 제안한다.
[Summary]

Dozerformer의 Dozer attention 프레임워크는 위와 같다.
먼저 다변량 시계열 예측(MTS)의 목표는 D개의 변수들의 I 개의 과거 시퀀스로 O개의 time step 을 예측하는 것이다. Dozerformer에서는 먼저 입력 데이터를 seasonal component와 trend component로 분리한다. 분리하는 방법은 이동 평균을 사용하여 시계열 데이터에서 트렌드와 계절성을 추출한다. 이후 입력 데이터 I개의 계절성과 트렌드로 O개의 time step을 예측한다. Dozerformer에서는 트렌드와 계절성을 각각 따로 예측한 후 Concatenate하고 RevIN을 적용하여 원래의 시계열 분포로 나타낸다.
● Seasonal Component
● DI Embed
계절성 요소는 DI Embed를 통해 다채널 특성 맵으로 변환된다. 이 변환은 시간 단계와 변수 차원을 모두 유지하면서 시계열 데이터를 모델에 적합하게 바꾸는 데 사용된다. Dozerformer에서 DI Embed는 MTS 데이터를 시간 단계 차원을 기준으로 여러 패치로 나눈다.
● Transformer Encoder
이렇게 분할된 패치 임베딩은 $ X_{enc} \in \mathbb{R}^{c\times N_{enc}\times p\times D}$로 나타내며 각 변수는 다음과 같은 의미를 가진다.
c : 특성 맵의 수. 여러 특성 맵을 만들어 시계열 데이터의 특성을 다채롭게 포착한다.
$N_{enc}$ : I/P, 인코더의 패치 수. I는 원본 시계열 데이터의 시간 단계 수이고 p는 패치의 크기이다.
p : 패치 크기. 원본 시계열을 여러 개의 작은 시간 구간으로 나눈다.
D : 각 패치의 차원. 각 패치가 갖는 특성의 수
이러한 패치는 시계열 데이터를 다루기 위해 트랜스포머 모델에 입력되는 데이터 형태로 변환된다.
● Transformer Decoder
디코더의 입력은 L 개의 이전 시간 단계와 O 개의 제로 패딩을 포함하여 생성된다. 디코더의 패치 수는 $N_{dec} = \frac{L+O}{p}$로 정의된다. 즉, 디코더의 입력 데이터는 이전 시점의 데이터와 패딩을 포함하여 패치로 변환된다.
L : 이전 시점의 데이터 개수
O : 제로 패딩의 수. 디코더의 입력 크기를 맞추기 위한 패딩
$N_{dec} : 디코더에서 생성된 패치의 수
트랜스포머 인코더와 디코더를 통해 계절성 요소의 주기적 특성을 패치 단위로 나타낸다. 얻은 결과값을 2d 차원의 컨볼루션 레이어를 적용하여 계절성 예측을 생성한다. 이 CNN은 트랜스포머로 얻은 정보들을 하나의 주기적 특성을 가지는 정보로 표현해준다.
● Trend Component
트렌드 요소는 이전 몇 개의 시점 데이터로 증가하는 추세인지 감소하는 추세인지를 파악하는 것이므로 Linear Layer를 통해 나타낸다.
여기까지가 어텐션 연산(트랜스포머 구조)를 이용하여 시계열 예측 과업을 수행하는 dozerformer의 방법론이다. 하지만 여기에는 한계점이 존재한다.
● Limitation
모두가 잘 알다시피 Query, Key, Value는 어텐션 연산에서 중요한 벡터이다. 이 벡터들은 입력 시퀀스인 $X_{d}^{enc}$에 대해 각각 임베딩을 통해 생성된다. 어텐션 연산은 두 가지 한계점이 존재한다. 먼저, 트랜스포머의 인코더는 시간복잡도가 제곱항 만큼 이므로 그만큼 시퀀스 길이가 짧아지게 된다. 두 번째로, 디코더의 크로스 어텐션 연산이 이전 모든 시점을 고려하여 연산하게 된다. 이전 몇 개의 time steps만 추출하여 사용한다 하더라도 어텐션 연산은 전체를 사용해야 하므로 여기에는 모순이 존재한다.
따라서 Dozerformer에서는 다음과 같은 방법을 제안한다.
모든 어텐션 연산을 수행하지 않기 위해 다음 세 가지 요소를 추출하여 어텐션 연산을 수행한다.

● Local
Local은 이전 시점의 정보만을 참고하도록 하는 요소이다. 구체적인 수식은 다음과 같다.

셀프 어텐션을 수행할 때 어텐션을 수행하는 i와 j 시점의 절대오차가 예측하려는 window size(w)의 절반보다 작거나 같은 경우에만 셀프 어텐션을 수행한다. 크로스 어텐션을 수행하는 경우에는 예측할 시점(t)와 j의 오차가 w의 절반보다 작거나 같은 경우에만 수행하도록 한다. 나머지의 경우에는 0으로 어텐션을 수행하지 않는다.
아래의 그림은 Local 조건을 적용한 예시이다. 윗 부분이 셀프 어텐션, 아랫 부분이 크로스 어텐션이다.

● Stride
Stride는 특정 주기의 정보만을 어텐션한 요소이다. 수식은 다음과 같다.

i와 j의 절대오차를 s로 나누었을 때 나누어 떨어지는 경우에만 어텐션 연산을 수행한다. 아래의 그림은 Stride 조건을 적용한 예시이다.

● Vary (Length)
Vary는 패치의 크기를 동적으로 조정하는 요소이다. 시계열 데이터의 시점이 늘어날수록 더 많은 정보가 필요할 수 있으므로 더 많은 시점의 정보를 사용하도록 하는 요소이다. 구체적인 수식은 다음과 같다.


Vary는 셀프 어텐션 부분을 정의하지 않는다. 당연하지만 셀프 어텐션에서는 고정된 범위 내에서 작동하기 때문에 Vary가 필요하지 않다.
세 가지 조건을 모두 적용한 결과이다.

회색이 아닌 부분이 어텐션이 수행되는 부분이다.
[Results]
● Datasets
ETTh1, ETTh2, ETTm1, ETTm2, Traffic, Electricity, Weather , Exchange-Rate, ILI 데이터셋으로 실험하였다.
● Baseline models
트랜스포머 기반의 방법들인 Informer, Autoformer, FEDformer, Pyraformer, Crossformer, PatchTST와 CNN 기반의 방법인 MICN, Linear 방법인 DLinear를 비교 모델로 선정, 실험하였다.
● 평가 지표
MSE, MAE
● 학습 세부 사항
Optimizer : Adam
학습률 : {5e-5, 1e-4, 5e-4, 1e-3} 중에 grid search로 코사인 어닐링을 통해 선정
트랜스포머 인코더 레이어 : 2
트랜스포머 디코더 레이어 : 1
window size : {96, 192, 336, 720} ( ILI : {120})
patch size : {24, 48, 96}
결과는 seed 1, 2022, 2023, 2024, 2025, 2026으로 학습한 결과의 평균으로 사용

● 결과
Dozerformer는 PatchTST보다 0.4%, DLinear보다 8.3%, MICN보다 20.6%, Crossformer보다 40.6% 낮은 MSE를 보여준다. PatchTST가 본인들의 결과와 유사한 성능을 보여주지만 PatchTST는 full attention을 사용한다는 점에서 덜 효과적이라고 주장한다.

아래는 파라미터 개수, FLOPs(floatin-point operations), 메모리(maximum GPU memory consumption)을 나타낸 표이다.

DLinear 모델을 사용하였을 때 가장 적은 파라미터, FLOPs, Memory를 사용한다. Dozerformer와 PatchTST를 비교했을 때 더 적은 자원으로 비슷한 수준의 예측을 수행한다는 것을 알 수 있다.
아래는 파라미터에 따른 각 모델의 성능 비교이다.

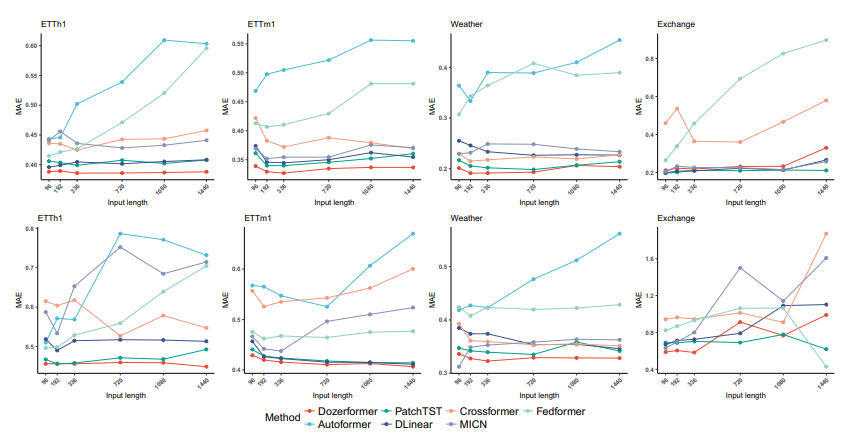
[Conclusions]
위 연구를 통해 시계열 예측 분야에서 시계열 데이터를 처리하는 attention을 새롭게 정의하여 Local, Stride, Vary의 조건에 해당하는 시점의 데이터들만 어텐션을 수행하여 더 적은 자원으로 현재의 SOTA 모델을 능가하는 성능을 보여주었다. 굳이 full attention을 수행하지 않고 시계열 데이터의 특성인 주기성에 해당하는 부분만 선택적으로 attention을 수행함으로써 제한된 자원에서도 시계열 예측 과업을 효과적으로 수행할 수 있다고 생각한다.
위 논문을 읽으면서 전통적인 시계열 예측 방법을 어텐션에 적용한 논문이라고 생각했다. 시계열 데이터의 특징을 추출하고, 시계열 데이터의 주기성을 파악하는 과정만 어텐션 기법을 사용함으로써 비용은 낮추고, 동일한 결과, 혹은 더 나은 결과를 얻을 수 있다는 점이 잘 설계한 논문이라고 생각했다.
[Reference]
Y.Zhang, et al., "Sparse Transformer with Local and Seasonal Adaptation for Multivariate Time Series Forecasting" arXiv:2312.06874



