[Paper Review] Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting

논문 리뷰

[Paper Review] Lag-Llama: Towards Foundation Models for Probabilistic Time Series Forecasting

ppid0930 2024. 9. 27. 16:13

[Background]

● 시계열 예측 연구

대규모 언어 모델(LLM)의 발전은 자연어 처리 및 컴퓨터 비전 분야에서 큰 영향력을 미쳤다. 이러한 LLM의 성공으로 시계열 예측을 LLM을 활용하여 해보면 어떤가 하는 연구가 계속해서 진행되고 있다. LLM을 활용하여 시계열 데이터를 예측하는 분야는 크게 두 가지로 나뉘게 된다. 하나는 LLM은 freeze한 상태로 두고 LLM에게 입력으로 제공하는 데이터를 LLM이 잘 예측할 수 있도록 언어의 형태로 변환하여 입력을 주는 방법이고 다른 하나는 아예 시계열 데이터를 잘 예측할 수 있는 foundation model을 생성하는 방법이다. 본 논문에서는 두 번째 방법인 LLM모델에서 영감을 얻어 Transformer구조의 Decoder 부분을 M번 반복하여 시계열 데이터를 예측하는 모델인 Lag-LLaMA에 대해 얘기한다.

● 시계열 데이터의 특성

시계열 데이터는 특징 값이 특정 시간 간격으로 기록되는 데이터를 만한다. 이러한 시계열 데이터에는 다른 유형의 데이터와 구별되는 몇 가지 특성이 존재한다.

시간 종속성(Time Dependence) : 시계열 데이터는 시간을 기준으로 정렬되며 데이터 포인트의 순서가 매우 중요하다. 각 관찰 값은 이전 관찰값과 미래 관찰 값에 따라 달라진다.
계절성(Seasonality) : 많은 시계열 데이터는 주기마다 데이터의 패턴이 반복된다. 이러한 패턴은 하루마다, 또는 주, 월, 년마다 반복적으로 나타날 수 있다.
추세(Trend) : 추세는 시간의 경과에 따른 데이터의 장기적인 움직임을 나타낸다. 최근 몇일 또는 몇 주 동안 데이터가 증가하는 추세인지 감소하는 추세, 또는 횡보(일정)하는 추세가 있다.
노이즈(Noise) : 노이즈는 어떤 패턴에 속하지 않는 튀는 값을 의미한다.
자기상관성(AutoCorrelation) : 자기 상관성은 데이터 포인트와 지연된 관찰 사이의 관계를 측정한다. 연속된 데이터 포인트 간의 유사도를 나타낸다.

● Foundation Model

Foundation model은 레이블이 지정되지 않은 광범위한 데이터 집합에 대해 훈련된 대규모 인공지능 모델로, 광범위한 다운스트림 작업에 적용할 수 있는 AI 모델 유형을 말한다. 일반적으로 self-supervised 방식으로 레이블이 지정되지 않은 광범위한 데이터 세트에 대해 사전 훈련되고 그 과정에서 일반화 가능하고 적응 가능한 데이터 표현을 학습하는 모든 모델이다.

Foundation model은 Emergence Behaviors와 Homogenization이라는 두 가지 특징을 가지고 있다. Emergence Behaivors는 하위 계층에 없는 특성이나 행동이 상위계층에서 자발적으로 돌연히 출현하는 현상으로 시스템의 행동이 직접 프로그래밍되는 것이 아니라 데이터를 통해 유추되기 때문에 생기는 현상이다. Homogenization은 많은 데이터를 통해 사전학습 시키면 이러한 거대한 지식을 압축시킨 단일화된 모델을 만들게 된다. 기존 LLM은 방대한 양의 Corpus 데이터를 학습하여 언어학적 지식을 압축한 모델인 것이다.

→ 시계열 데이터를 처리하는 Foundation Model 다양한 대규모 시계열 데이터에 대한 학습과, 다양한 시계열 데이터의 다양한 Frequency에 대해 대응해야하며 Downstream task에 적용할 때 모델이 Unseen Frequency와 Seen Frequency의 조합을 다룰 수 있어야 하며 특정 데이터셋의 Frequency에 의존하지 않고 데이터셋의 Series를 토큰화하여 Unseen Frequency와 Seen Frequency의 조합을 테스트에서 적용할 수 있는 일반적인 방법을 제시해야 한다.

[Summary]

본 논문에서 주장하는 시계열 데이터 예측을 위한 Foundation Model인 Lag-LLaMA는 다음과 같은 과정을 통해 학습하였다.

1. 사전 학습(Pre-training)

먼저 Foundation Model을 생성하기 위해 본 논문에서는 Lag-LLaMA를 사전 학습하기 위한 다양한 도메인의 27개의 시계열 데이터셋을 사용하였다. 각 데이터셋들은 서로 다른 길이와 주기를 가지며, 각 분야별로 같은 그룹으로 분류하였다. 데이터셋들이 서로 다른 길이와 주기를 가지므로 표준화 과정을 통해 데이터의 스케일을 맞춰줘야 한다. 본 논문에서는 Robust Standardization을 사용한다. 표준화 과정을 거친 데이터는 Lagged features와 Date time features를 추출하고 고차원 벡터로 결합하여 모델에 입력된다.

● Robust Standardization

Robust Standardization은 표준적인 Z-score standardization과 달리 이상치에 강력하도록 설계되었다. Robust Standardization은 중앙값과 사분위 범위(IQR)를 사용하여 데이터의 변동성을 줄인다. 먼저 중앙값을 구한 후, 각 데이터포인트에서 중앙값을 뺀다. 그 후에 사분위 범위를 구하여 데이터를 IQR로 나누어 스케일링 한다. 이 방식은 데이터가 이상치를 포함하더라도 모델이 데이터를 안정적으로 학습할 수 있도록 한다.

표준화된 데이터는 예측 결과를 해석할 때 역변환되며 학습 중 사용했던 중앙값과 IQR을 이용하여 데이터를 다시 원래 범위로 변환한다.

● Lagged Features

Lagged features는 과거 시점의 데이터를 이용하여 현재 또는 미래 시점을 예측할 수 있도록 이전 데이터를 지연된 형태로 변환하는 과정이다. 어떤 특정 시간 t에서의 값을 예측할 때, 이전 n개의 시점의 데이터를 참조한다. 여기서 이전 시점 데이터를 참조하는 간격이 Lag가 된다. 그러면 당연히 Lag 간격을 설정하는 것이 t시간에서의 값을 예측하는 것에 큰 영향을 끼칠 것이다. 여기서 Lag 간격은 단순히 바로 이전 시점만을 사용하는 것이 아니라 다양한 간격의 Lag를 설정하여 다중 시점의 데이터를 활용한다.

이렇게 수집된 Lag 데이터를 벡터로 변환한다. 예를 들어 $x_{t}$ 시점에서 이전 t-1, t-7, t-30 시점의 데이터를 Lag를 통해 수집했다면 각 시점의 데이터를 각각 벡터로 변환하고 이를 하나의 고차원 벡터로 결합하여 모델에 입력한다.결합할 때 Lag 데이터만 결합되는 것이 아니라 시간적 맥락 정보도 추가되어 각 시점의 정보가 입력에 포함된다. 이 벡터는 Linear Projection을 통해 고차원으로 변환되고, 변환이 완료된 벡터는 Transformer의 디코더 부분에서 처리된다.

2. 선형 투영(Linear Projection)

저차원 데이터인 시계열 데이터를 고차원 벡터로 변환하는 방법이다. 예를 들어, Lag 특성 벡터의 차원이 10이라면 이 벡터를 선형 투영을 통해 512차원이나 1024차원의 고차원 벡터로 변환하게 된다. 이때 가중치 행렬 W는 입력 벡터를 고차원 벡터로 변환하는 역할을 한다. 이 가중치 행렬은 학습 과정에서 모델이 데이터를 잘 표현할 수 있도록 학습 가능한 파라미터로 업데이트된다. 아까와 같은 예시로 Lag 특성 벡터의 차원이 10이라면 512 차원으로 변환하기 위해서 가중치 행렬 W는 10 x 512의 크기를 가지게 되고 1024 차원으로 변환하기 위해서는 가중치 행렬 W는 10 x 1024의 크기를 가지게 된다.

3. 모델 입력

고차원 벡터로 변환한 시계열 데이터를 이제 모델에 입력한다. 시계열 데이터를 예측하기 위해 사용되는 트랜스포머 모델은 모든 입력 시점 데이터를 동시에 처리할 수 있지만 미래 정보를 사용하지 않아야 한다. 이를 위해 마스킹된 자기회귀 방식을 사용한다. 이는 미래 시점의 데이터를 차단하고, 과거의 데이터만을 기반으로 예측을 진행하도록 한다. 또한 트랜스포머의 구성요소인 어텐션 메커니즘을 사용하여 각 시점에서 다른 시점 간의 상호작용을 고려하여 각 시점의 데이터와 다른 시점의 데이터 간의 관계를 파악한다. 어텐션 메커니즘은 데이터의 순서 정보를 알지 못하기 때문에 시계열 데이터의 시간 정보를 전달해주기 위해 RoPE(Rotary Positional Encoding)을 수행한다. 이는 시계열 데이터에서 시간의 상대적 위치 정보를 학습할 수 있도록 하여 특정 시점에서 이점 시점들 간의 상대적 차이를 더 잘 반영할 수 있게 돕는다. 어텐션 메커니즘을 사용한 후에는 안정적인 학습을 위해 정규화를 적용한다. Lag-LLaMA의 경우, RMSNorm을 사용하여 정규화한다. 이 단계를 총 M번 반복하여 더 깊은 학습을 수행한다.

4. 분포 헤드(Distribution Head) 학습

Transformer layer를 통과한 데이터는 분포 헤드로 전달되어 확률 분포의 매개변수로 변환된다. 이 과정에서 예측된 미래 값이 확률적 형태로 출력된다. 해당 논문에서는 다양한 분포들 중 Student t-분포를 채택하고 해당 분포의 매개변수(평균, 분산, 자유도) 를 예측한다. 여기서 예측이라는 표현을 사용하여 이해에 어려움이 있을 수 있는데, 지금 하려는 것이 해당 시간대의 시계열 데이터를 예측하려는 것이기 때문에 예측하려는 시간대에 대한 확률 분포의 평균, 분산, 자유도를 예측한다고 이해하면 된다. 따라서 더 먼 시간대를 예측할수록 이 확률 분포가 더 고르게 분포되게 된다. 여기서 평균은 모델이 t 시간에서 가장 가능성이 높은 예측값을 나타내고 분산은 t 시간의 예측값이 얼마나 변동할지를 설명한다. 자유도는 극단적인 값이나 예외적인 값들이 얼마나 나올 가능성이 있는지를 반영한다.

5. 손실 함수 계산

Lag-LLaMA 모델의 경우, 확률적 시계열 예측을 수행하기 때문에 예측값의 형태가 확률 분포의 형태로 나타난다. 이러한 확률 분포의 손실 값을 측정하기 위해 부정 로그 우도(Negative Log-Likelihood)를 사용한다.

● Log-Likelihood & Negative Log-Likelihood

Log-Likelihood는 모델이 예측한 확률 분포와 실제 관측된 데이터 사이의 일치도를 평가하는 방법이다. 주어진 실제 관측 값이 모델이 예측한 확률 분포에서 얼마나 높은 가능성을 가지는지 평가하는데, 이를 극대화하는 것이 목적이다.

$$LL = \sum logP(y_{i}|\theta )$$

Negative Log-Likelihood는 Log-Likelihood의 음수이다. 즉, 모델이 예측한 값이 실제 값과 얼마나 불일치하는지 평가하며, 손실 함수로 사용된다. 모델의 성능을 높이기 위해서는 이 값을 최소화해야 한다.

$$NLL = -\sum logP(y_{i}|\theta )$$

6. 최적화

손실 함수 값을 계산하고 계산된 손실 함수를 최소화하는 방향으로 모델의 파라미터가 조정되도록 하는 과정이다. 본 논문에서 최적화 방식에 대해 언급된 부분은 없지만 Transformer 모델 및 딥러닝 모델에서 대부분 Adam을 사용하므로 아마 Adam이 최적화 알고리즘으로 사용되지 않았을까 생각한다.

[Results]

본 논문에서는 Lag-LLaMA를 테스트하기 위해 다양한 출처에서 가져온 27개의 시계열 데이터셋을 사용하여 모델을 훈련하고 평가한다. 주요 도메인은 에너지, 교통, 경제학, 자연, 공기질, 클라우드 운영이다. 각각의 데이터셋은 예측 길이, 시계열 개수, 시계열 길이, 데이터 수집 주기 등이 다르다. 사전 학습에서는 대부분의 데이터셋을 사용하지만 일부 데이터셋은 사전 학습에 포함하지 않고 테스트를 위해 남겨두었다. 그래서 7,965개의 서로 다른 시계열이 사전 학습에 사용되었으며, 총 약 3억 5200만개의 데이터 토큰이 모델을 훈련하는 데 사용되었다. 또한 다양한 예측 지평선을 고려하여 단기, 중기, 장기 예측을 평가한다.

비교 모델로는 통계적 시계열 예측 모델, 딥러닝 기반 시계열 예측 모델, 다른 트랜스포머 및 딥러닝 모델을 사용하였다. 모든 모델은 확률적 예측을 수행할 수 있도록 AutoGluon을 통해 사용되었다. 일부 모델은 점 예측과 정규화된 데이터를 사용하도록 설계되었지만, 실험에서는 확률적 예측이 가능하도록 출력에 분포 헤드를 추가하여 Lag-LLaMA와 동일하게 설정하였다.

각 모델을 사용하여 CRPS를 계산한 결과이다. CRPS는 예측된 확률 분포와 실제 값 사이의 차이를 측정하며, 단일 예측 값이 아닌 예측 분포를 평가할 때 주로 사용된다.

이 표는 Lag-LLaMA가 Zero-shot 성능과 Fine-tuning 성능을 새로운 데이터에서 평가한 결과이다. Lag-LLaMA는 평균 순위 6.714를 기록하며, 사전 학습된 모델임에도 불구하고 특정 데이터셋에 맞춰 학습된 모델들과 거의 비슷한 성능을 보여주었다. Fine-tuning 한 Lag-LLaMA의 경우, Weather, ETT-M2, Requests 데이터셋에서 sota를 달성했으며 다른 모든 데이터셋에서도 Zero-shot과 비교해 보았을 때 성능이 크게 향상되었다. 여기서 One Fits All 모델과도 비교를 진행하는데 Lag-LLaMA가 모든 면에서 좋은 성능을 보여주었다.

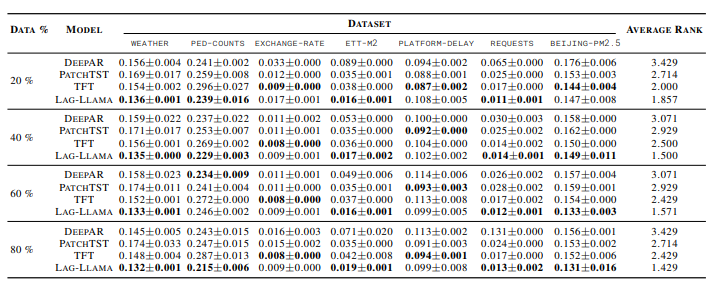
이 표는 각 모델의 few-shot 적응 능력을 평가한 표이다. 실험에서는 데이터셋의 훈련 세트에서 마지막 K%의 데이터만을 사용하여 실험을 진행하였다. 지도 학습 모델들은 해당 데이터에서 처음부터 훈련을 시작했지만, Lag-LLaMA는 사전 학습된 모델을 Fine-tuning 하여 평가하였다.

few-shot 실험에서 Lag-LLaMA는 다른 모델들보다 더 높은 성능을 기록하였다. 하지만 일부 데이터셋에서는 좋은 모습을 보여주지 못했는데 해당 데이터셋은 새로운 도메인이며, 사전 학습된 데이터와 다른 주파수 패턴을 가지고 있기 때문에 성능이 낮을 수 있다고 한다. 결과적으로 Lag-LLaMA는 적은 양의 데이터에서도 우수한 성능을 보여주며, 데이터의 양이 증가할 수록 성능이 크게 향상된다는 것을 증명하였다.

[Conclusions]

본 논문에서 주장하는 Lag-LLaMA는 트랜스포머 구조를 활용하여 기존에 없는 시계열 데이터를 다루는 Foundation Model을 만들어 낸 것에 매우 큰 의의가 있다. 또한 사전 학습 시키지 않은 데이터셋에 대해서도 다른 모델들과 비교했을 때 상당히 높은 성능을 보여주었다.

사실 어떤 모델들 보다도 성능이 좋을 것 같은 생각이 논문을 읽으면서 계속 들었다. 자연어 처리 분야에서도 말뭉치가 많으면 많을 수록, 학습을 많이 시킬 수록 좋은 성능을 보여주었던 것처럼 Lag-LLaMA도 20개 남짓의 시계열 데이터셋을 학습시켰음에도 좋은 결과를 보여주었으므로 더 많은 시계열 데이터에 대해서 학습을 시킨다면 어쩌면 시계열 데이터만 보고도 어떤 데이터셋인지 예측하거나 미래를 잘 예측할 수 있을 것이라 생각한다.

본 논문에서 Distribution Head를 Student t-분포를 사용하였는데 t 분포는 대표적인 정규분포이다. 하지만 예측하려는 데이터셋의 특징에 따라 결과값이 달라질 수 있다. 본 논문에서도 이 분포를 어떻게 할 것인지에 대한 연구는 후속 연구로 남겨두었다.

Lag-LLaMA의 성능을 결정하는 것에는 여러가지 요인이 존재한다. 첫 번째로 Lag window 설정이다. Lag의 window 값을 유동적으로 설정하는 것이 아니라 모든 데이터셋에 대해 동일한 길이의 Lag을 설정하도록 하다 보니 일부 시계열 데이터셋에는 충분한 데이터셋이 제공되지 않을 수 있다. 또한 사전 학습된 데이터와 크게 다른 도메인이나 주파수 패턴을 가진 데이터셋에는 잘 예측하지 못하는 것을 보여주었다(Exchange 데이터셋). 아무래도 많은 데이터를 학습하므로 학습 시간이 오래 걸릴 수밖에 없다는 단점이 있다.

시계열 데이터를 예측하는 Foundation Model에 대해 다룬 논문에 대해 찾고 있었는데 여러 단점에도 불구하고 찾고 싶었던 논문을 읽게 되어 마음이 풍족해진 느낌이다. :)